Is Walter Lewin wrong about Kirchhoff's law?
Thinking how to organize the upcoming material about geometry and physics I came about a recent controversy about an electromagnetism lecture by Walter Lewin and I want to talk about it in this post.
First, a little background. When I started teaching undergraduate physics I needed help on how to structure the lectures. Personally I wanted to emulate Feynman lectures, but the physics departments impose on you either Giancolli or Young and Friedman. I turned to internet for help and I found the outstanding undergrad lectures by Walter Lewin which I adapted to my needs - thank you Professor Lewin. In lesson 16 on electromagnet induction which you can watch below
on minute 34:54 the fireworks begins. The setup starts unassuming: a trivial circuit with a 1 V battery and two resistors in series. The current is computed as well as the voltage drop across the larger resistor. Then the battery is removed and is replaced by a solenoid in the middle of the circuit which generates an increasing magnetic field such that the induced voltage is the same 1 V as the battery. Now the question becomes: what is the voltage drop on each resistors? The answer is that two voltmeters connected on the same points one on one side of the loop and one of the other side will record different voltages of opposite polarities! In this case one will record +0.9 V and the other -0.1 V. And the experiment confirms this!!!
For a complete step-by-step derivation see: web.mit.edu/8.02/www/Spring02/lectures/lecsup3-15.pdf
This is deeply at odds with our intuition and there are a lot of "proofs" of why Lewin is wrong. Here is one example which has the advantage over others that it is in English.
Lewin responded to those challenges in two distinct posts in a poor manner in my opinion: he simply repeated slowly and loudly his explanation and did not address the root cause of the discomfort people experience when presented with this counter-intuitive phenomena. So I will attempt to add my own pedagogical explanation of how to understand this.
First, are the two voltmeters connected on the same points? It is not clearly visible on the video how the two voltmeters are connected, but if you have access to an electronics lab you can actually connect the two voltmeters on the very same points and repeat the experiment. So how is it possible that two identical voltmeters connected to the same points read something differently? This is because different currents flow through the two voltmeters.
Now you may say: this is absurd, why different currents flow through the two voltmeters? Can I just simply use only one voltmeter and place it on the right hand side of the circuit, and then flip it to the left hand side? Why would the reading change?
The reading does not change as long as you do not cross the changing magnetic field zone. However as you cross the changing magnetic field the voltmeter reading changes gradually from the right hand side value of +0.9 V to the left hand side value of -0.1 V. We can actually compute how this happens and I will do it below.
But before doing it, I want to say what is wrong in the "disproof" video above. First, the solenoid is the same size of the circuit and is placed under the circuit. This allows for the gradual voltage change due to crossing of the changing magnetic field to be misinterpreted as a voltage drop on the copper wiring. Second, the explanation is inconsistent with regards to the current intensities. If you compute the intensity in the copper wire due to 1 V difference you do not get 1 milli Ampers, but a huge current because copper wire has almost zero resistance. Also there is a big misunderstanding on the how to compute the flux by stating that a vertical plane has no flux going though it. If the loop would be completely vertical this would have been correct, but the the voltmeter loop also contains a horizontal path closing the circuit and this has non-zero magnetic flux crossing through it.
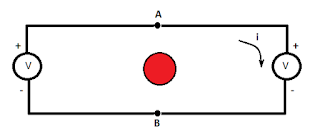
So now onto the computation. I will use only one voltmeter which is placed on the right like in the first picture below:
Then I move the connection points A and B and flip the voltmeter wire to cross the magnetic region (see the second picture and notice that the direction of i stays the same: from the voltmeter to r2).
Let's work out the math in the first case. There are two loops with currents I and i and the resistance of the voltmeter is R >> r1, r2:
I(r1+r1) - i r2= E (induction law)
i r2 - I r2 + i R = 0 (Kirchhoff)
in the second equation r2 << R and we can ignore the first term: -I r2 + i R = 0 which means i << I and in the first equation we can ignore the negative term resulting in:
I (r1 + r2) = E from which we extract the current in the main loop.
Then V read by the voltmeter is V = i R = I r2 = E r2 /(r1+r2) = 0.9 V using the resistors and E value from the lecture.
Now we are proceeding to flip the voltmeter from right to the left. Suppose that during flipping we cross s% of the changing magnetic flux area (the yellow area) with the voltmeter loop. The first equation reads as before:
I(r1+r1) - i r2= E (induction law)
but the second one is changed to:
i r2 - I r2 + i R = -sE (induction law)
the same order of magnitude tricks apply and we get:
I (r1 + r2) = E
-I r2 + i R = - sE
and the voltage recorded by the voltmeter is V = i R = I r2 - sE
V = E r2 /(r1+r2) - sE with \(s \in (0,1)\)
So on the right side the voltmeter reads E r2 /(r1+r2) = 0.9 V and on the left side the voltmeter reads
E r2 /(r1+r2) -E = -E r1/(r1 + r2) = -0.1 V with all the intermediate values in between as we flip the device.
This effect is shown in Mabilde's video from 17:40 to 18:00, but his explanation is wrong.
Alternatively when the voltmeter is flipped all the way to the left we can consider a loop not enclosing the area of changing magnetic field and arrive at the same -0.1 V by using Kirchhoff's just like we did on the right hand side.
If we consider two left and right voltmeters we can also understand why they record different values. We can consider the outer loop and apply the induction law to it and see that a current "i" flows from one voltmeter through the other due to the area of changing magnetic field. Since the voltmeters are polarity sensitive one would record a positive voltage and another one a negative voltage. In fact we can further simplify the setting by removing the two resistors completely and in this case one voltmeter would record +0.5 V and another -0.5 V:
In conclusion the Walter Lewin is completely correct and the controversy stems from blind trust in Kirchhoff's circuit laws which are valid only when there is no changing of magnetic flux in the circuits and a misunderstanding of Maxwell's equations.

Hallo Mr. Moldoveanu. You wrote: “If you compute the intensity in the copper wire due to 1 V difference you do not get 1 milli Ampere, but a huge current because copper wire has almost zero resistance.” This is a big mistake! You make a mix of DC and AC! I have proven this in my video:www.youtube.com/watch?v=v85ln_l0fcE&t=1209s . You were right, if in this circuit is a DC voltage, but the changing magnetic flux creates an AC voltage! In that case the copper wires acts the same way as wires in a transformer! Each wire in this circuit will produce 0.5V. Also the resistors take part in this circuit. Also the resistors will produce a very small voltage, but this is negligible comparing with the voltage produced in the wires. Best regards, Dirk
ReplyDeleteHi Dirk, Happy New Year!
DeleteSorry, I cannot understand your video because it is not in English. However I made no mistake. Imagine that the changing magnetic flux happens on a constant rate for say 10 seconds. During that time you are effectively in the DC domain.
Best,
Florin
Hallo Mr. Florin, I wish you a very happy new year too! It is easy to switch on the English subtitles. Below the video, you have a "display bar". On the right, you have an icon to switch on the English subtitles. Normally the subtitles start automatically, but if they don't, you can handle this manually.
ReplyDeleteTo remain a DC voltage in a coil with a pulse for 10 seconds, would be impossible. As you can watch Mr. Lewin's video, in his experiment he switches a DC current over his primary coil. This creates only a pulse of 0.1ms in his secondary circuit, while the DC voltage on his primary coil remains! This secundary pulse is according AC-laws! If you succeed to switch on the subtitles of my video, it will become very clear to you, because it is shown in practice that the wires produce a voltage, because of the AC pulse! And you are iright, if a DC would remain for 10s, there would be a high current, and it would heat up the wire, according to DC-laws. But that isn't the case at all in this experiment. Kind regards, Dirk
Hello Dirk, I finally got a chance to watch your you tube video with the captions. There are many issues with your explanations:
Delete1. straw man argument. The Lewin experiment is supposed to be done in the DC range with an increasing magnetic flux of constant slope, not with AC current.
2. The A,B,C,D connections are not clearly traceable in the video. There is a tangled mess on the table and a camera has to be placed directly above the table with a person clearly tracing the wires, otherwise it is easy to fake any results you like.
3. the missing negative pulse. I suspect you measure only the positive signal and on connect (BC and DA) and on disconnect AB and BC. If so the math of zero total voltage is bogus as it does not happen at the same time. The voltage on AB and BC can be induced from the magnetic changing field from the ABCD loop itself.
4. the explanation on 1:13:00 is completely wrong. Here you are arguing against a mathematical theorem: Stokes theorem with a bad example. What counts is the total magnetic flux through the surface. When you place the coil generating B in the middle most of the magnetic field closes on itself and the total flux (to any surface encompassing the big wire loop) is close to zero.
Now there is a simple falsifiability test. I will admit I am wrong if you can derive Kirchhoff's law in the case of a DC circuit from Maxwell's equations when a changing magnetic flux going through your circuit - it can't be done, is a mathematical impossibility.
Alternatively I will admit I am wrong if you do a DC experiment (in a way which can be repeated by any critic - I do have access to an electronics lab and I will be able to recreate it) and show a drop in voltage in between the resistors.
Sorry I discovered two errors in my reply:
ReplyDeletein 1. it must be:<>
Very sorry for professor Lewin: he understands only one aspect of Faraday's law when he defines the EMF only in the resistors. He apparently can not distinguish between cause and effect . The EMF is the "cause" (of the induced current) and this same current, passing through the load resistor, creates the voltage drop across the resistor. And that is the "effect". For him an EMF is something like a ghost, coming from nowhere, invisible, having only an effect , but for the rest at least incomprehensible "to someone with very little knowledge of physics" like me and Dirk. Thank you!
in 2: must be <> I forgot: "plane"
Additional comment to Mr Florin:
If you apply Ohm's law on a zero-Ohm wire, carrying an EMF and pretend that this should result in an infinite current, then again, you see or miss half of the picture, because the current is determined by the load resistor. You can not apply Ohm's law to one half of a series circuit and deny on the other part. If you have ideas for additional measurements that could be done on the REAL LEWIN COIL , please let me know. I'll do what you want to see and show it in a next video,so that everyone and also professor Lewin can benefit from it.
With friendly greetings from Belgium
Hi Cyriel
DeleteYou stated: "If you apply Ohm's law on a zero-Ohm wire, carrying an EMF and pretend that this should result in an infinite current, then again, you see or miss half of the picture, because the current is determined by the load resistor. You can not apply Ohm's law to one half of a series circuit and deny on the other part."
I am confused, this exactly is my criticism of your explanation. Ohm's law applies universally. In the wire with zero resistance there is no voltage drop. Pick any two points on the top wire and connect a voltmeter to it in such a way that it will not intersect the magnetic field. You will get a measurement of zero. In your particular setup you will get a non-zero voltage because your coil under the circuit is the size of the circuit and you will catch a changing magnetic field. Make the circuit say 10x larger and reduce the diameter of the coil say by 10 times and you will not pick up any voltage drop on the top wire.
I know this post is a little late, but how can you have current flow though a wire with zero resistance if there is not a potential difference across it? Does that mean a zero resistance wire acts as a open contact? I also hear arguments about how others have shown that Kirchoffs rule does work but are criticized for not following Walter Lewins example. Why are these experiments constrained to limits set forth by Walter Lewins. Either Kirchoff rule does not apply or does. I must be one of the ones that have a religious belief that Kirchoffs rule applies in the example he demonstrated in lecture 16. Why do I believe this? The induced electromotive force has to be reduced to 0 in a circuit, if not the current will continue to flow. It seems to me that what Walter Lewin is shown as EMF is the voltage drop. If what I am saying is wrong, I have a great idea, Take out the resistor 2, and then we will gain voltage in absents of a magnetic field. In my mind the induced EMF, which I consider the induced electric pressure, is dropped across the resisters that the current flows though. Please tell me how this is wrong?
Delete